Случайные процессы и их характеристики Задачи с решениями

Показать, что формулу Пуассона, определяющую вероятность появления k событий за время длительностью t

можно рассматривать как математическую модель простейшего потока событий; другими словами, показать, что формула Пуассона отражает все свойства простейшего потока.

Среднее число заказов такси, поступающих на диспетчерский пункт в одну минуту, равно трем. Найти вероятность того, что за 2мин поступит: а) четыре вызова; б) менее четырех вызовов; в) не менее четырех вызовов.

Среднее число вызовов, поступающих на АТС в одну минуту, равно двум. Найти вероятность того, что за 4 мин поступит: а) три вызова; б) менее трех вызовов; в) не менее трех вызовов. Поток вызовов предполагается простейшим.

Среднее число вызовов, поступающих на АТС в одну минуту, равно двум. Найти вероятность того, что за 4 мин поступит: а) три вызова; б) менее трех вызовов; в) не менее трех вызовов. Поток вызовов предполагается простейшим.

Задана интенсивность простейшего потока λ=5. Найти: а) математическое ожидание; б) дисперсию; в) среднеквадратическое отклонение непрерывной случайной величины Т -времени между появлениями двух последовательных событий потока.

Случайный процесс определяется формулой X(t)=XCos(ωt), где X — случайная величина. Найти основные характеристики этого процесса, если М(Х)=а, D(Х)=σ².

Построить граф состояний следующего случайного процесса: устройство S состоит из двух узлов, каждый из которых в случайный момент времени может выйти из строя, после чего мгновенно начинается ремонт узла, продолжающий заранее неизвестное случайное время.

На автоматическую телефонную станцию поступает простейший поток вызовов с интенсивностью λ=1,2 вызовов в минуту. Найти вероятность того, что за две минуты а) не придет ни одного вызова; б) придет ровно один вызов; в) придет хотя бы один вызов.

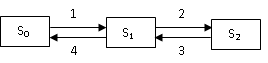
Найти предельные вероятности для системы S из примера 7.2, граф состояний которой приведен на рисунке, при λ₀₁=1, λ₀₂=2, λ₁₀=2, λ₁₃=2, λ₂₀=3, λ₂₃=1, λ₃₁=3, λ₃₂=2.

Найти средний чистый доход от эксплуатации в стационарном режиме системы S в условиях примеров 7.2 и 7.4, если известно, что в единицу времени исправная работа первого и второго узлов приносит доход соответственно 10 и 6 ден.ед, а их ремонт требует затрат соответственно в 4 и 2 ден.ед. Оценить экономическую эффективность имеющей возможности уменьшения вдвое среднего времени ремонта каждого из двух узлов, если при этом придется вдвое увеличить затраты на ремонт каждого узла (в единицу времени).

Процесс гибели и размножения представлен графом (рисунок). Найти предельные вероятности состояний.

Известно, что заявки на телефонные переговоры в телевизионном ателье поступают с интенсивностью λ, равной 90 заявок в час, а средняя продолжительность разговора по телефону t_об=2мин. Определить показатели эффективности работы СМО (телефонной связи) при наличии одного телефонного номера.

В условиях примера 7.7 определить оптимальное число телефонных номеров в телевизионном ателье, если условием оптимальности считать удовлетворение из каждых 100 заявок на переговоры в среднем не менее 90 заявок.

В вычислительный центр коллективного пользования с тремя ЭВМ поступают заказы от предприятий на вычислительные работы. Если работают все три ЭВМ, то вновь поступающий заказ не принимается, и предприятие вынуждено обратиться в другой вычислительный центр. Среднее время работы с одним заказом составляет 3ч. Интенсивность потока заявок 0,25(1/ч). Найти предельные вероятности состояний и показатели эффективности работы вычислительного центра.

Случайный процесс определяется формулой X(t)=Xe^-t (t>0), где X — случайная величина, распределенная по нормальному закону с параметрами а и σ². Найти математическое ожидание, дисперсию, корреляционную и нормированную корреляционную функции случайного процесса.

Среднее число заказов на такси, поступающих на диспетчерский пункт в одну минуту, равно 3. Найти вероятность того, что за две минуты поступит: а) 4 вызова; б) хотя бы один; в) ни одного вызова. (Поток заявок простейший.)

Рассматривается круглосуточная работа пункта проведения профилактического осмотра автомашин с одним каналом (одной группой проведения осмотра). На осмотр и выявление дефектов каждой машины затрачивается в среднем 0,5 ч. На осмотр поступает в среднем 36 машин в сутки. Потоки заявок и обслуживании — простейшие. Если машина, прибывшая в пункт осмотра, не застает ни одного канала свободным, она покидает пункт осмотра не обслуженной. Определить предельные вероятности состояний и характеристики обслуживания профилактического пункта осмотра.

Решить задачу 7.15 для случая n=4 канала (групп проведения осмотра). Найти минимальное число каналов, при котором относительная пропускная способность пункта осмотра будет не менее 0,9.

Задача 7.15: Рассматривается круглосуточная работа пункта проведения профилактического осмотра автомашин с одним каналом (одной группой проведения осмотра). На осмотр и выявление дефектов каждой машины затрачивается в среднем 0,5 ч. На осмотр поступает в среднем 36 машин в сутки. Потоки заявок и обслуживания — простейшие. Если машина, прибывшая в пункт осмотра, не застает ни одного канала свободным, она покидает пункт осмотра не обслуженной. Определить предельные вероятности состояний и характеристики обслуживания профилактического пункта осмотра.